DEMADJ: A Macro for Demand Matrix Adjustment Using Observed Volumes

(contributed by Heinz Spiess, EMME/2 Support Center)

In most transportation planning applications, the input data which is the most difficult and expensive to obtain is the origin-destination demand matrix. Since the demand data cannot be observed directly, it must be collected by carrying out elaborate and expensive surveys, involving home- or road-based interviews or complicated number plate tagging schemes. By contrast, observed link volumes can be obtained easily and with reasonable precision by simply counting the traffic at certain count post links, either manually or automatically, using mechanical or inductive counting devices.

Thus, it is not surprising that a considerable amount of research has been carried out to investigate the possibility of estimating or improving an origin-destination demand matrix with observed volumes on the links of the considered network. While the models proposed in the past differ greatly in their mathematical formulation and interpretation, they all share the fact that using them for real size networks is difficult, if not impossible. This is due to the complexity of the computations that are involved and the need for very specialized software to carry them out.

During the last two years, we have developed a new approach for the matrix adjustment problem. It is based on the gradient method: While minimizing an objective function based on the difference of observed - predicted volumes on the count post links, the concept of steepest descent, which is inherent to the gradient approach, ensures that the initial demand matrix is not changed more than necessary. The mathematical details of this new method are described in a separate publication (Spiess H., A Gradient Approach for the O-D Matrix Adjustment Problem, CRT Publication #693).

Most important from the practical point of view, is the fact that this method can be implemented as a macro in EMME/2 without the need of any additional software! This also implies that the method can be applied to any network and matrix size that can be handled in EMME/2. The implementation of one iteration of the adjustment method consists in a normal auto assignment, two Additional Options auto assignments, as well as several with network and matrix calculations. A scattergram of the observed vs. assigned volumes on the count post links is generated for each iteration; this facilitates monitoring the progress of the adjustment process.

During 1988 and 1989, we had the opportunity to test the proposed gradient method and apply it in practice in several studies. The test example used was based on the standard EMME/2 Winnipeg Demonstration Database. The applications include two urban applications for the cities of Bern and Basel (in collaboration with Rapp AG) and the two national road networks of Sweden (with Transek AB) and Finland (with Finnmap OY) The table below gives some characteristics of these applications: number of traffic zones, number of network links, number of links with observed volumes, the -value between observed and assigned volumes using the initial demand, the -value after the adjustment, and, finally, the number of gradient iterations that were carried out for the adjustment.

Study Zones Links Counts Iter.

Winnipeg 154 2983 70 0.834 0.971 11

Basel 330 220 229 0.923 0.970 6

Bern 226 2676 338 0.960 0.995 20

Sweden 522 3879 334 0.827 0.992 20

Finland 469 12476 5759 0.491 0.886 30

As an example, the scattergrams of observed versus assigned volumes before and after 20 iterations of the adjustment procedure are shown below for the Swedish national road network application. The computations were carried out on a SUN SPARCstation 1 computer. On this equipment, each iteration of the gradient method took about 25 minutes of computing time.

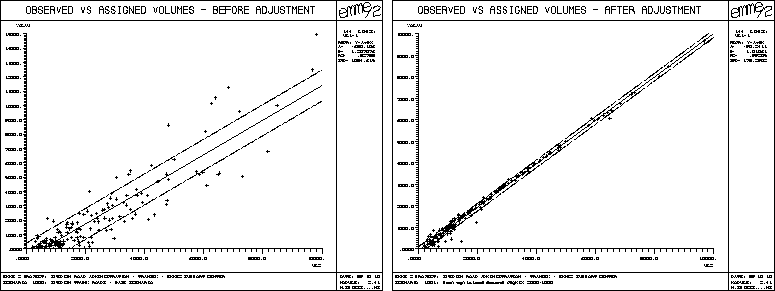
In all applications that were carried out so far, the gradient method was found to perform very well. However, there are some important practical points to consider before applying the algorithm:

• This model will adjust the demand matrix in order to better reflect the observed volumes. It should only be applied if all the other data which are used for the assignment have been extensively validated. The adjustment procedure will attempt to compensate any remaining error in the network coding, the volume delay functions or the observed volumes by modifying the demand matrix. This, of course, will not correct the error, but just add another error on top of it.
• The selection of the count post links is very important. Before applying the adjustment procedure, it is good practice to perform a rigorous count post analysis (this can also be carried out very elegantly using the additional options assignment feature of EMME/2). The count posts links should cover the network sufficiently, so that most trips will at least be counted once. Also the count post links should not carry a lot of local (= intrazonal) trips, since these will not be accounted for in the assignment. Finally, great care must be taken when the count post links are close to important connector links, since these are aggregated abstract trip ends which do not represent the true final destinations.
• Do not expect the observed volumes necessarily to form a consistent set. Inconsistencies can be due to inaccurate or non-simultaneous counts. But besides the imprecisions of the actual counting, inconsistencies can also arise from the zonal aggregation itself, which forces all trip ends to be at the centroid nodes. The counted volumes, however, are based on the true origin and destination of every trip. One should therefore not expect that the objective function Z must necessarily converge to zero.
• Once the adjustment has been carried out, it is crucial to analyze the results carefully and critically. We expect the change in the demand to be small and unsystematic. Large or systematic changes will almost always be an indication of a problem in the input data. Also, the comparison of the trip length histograms before and after the adjustment has proven to be very valuable. In all applications so far the analysis of the first runs of the gradient method has lead to the discovery of network coding problems - even though some of the networks have been used for years.
• Every time corrections are made to the input data, the gradient method should be restarted with the initial demand matrix. Technically, it would be possible to make changes to the network or the observed volumes between iterations of the gradient method and then continue. But this would defeat the key property of the gradient method, which is to find a solution with minimal change to the initial demand.

The macro DEMADJ is called in the following way:

~<demadj gqp dpq iter relgap normgap gstep [cnt]

The parameter are defined as follows:

gpq

Demand matrix to be adjusted (e.g. "mf6"). Since the initial contents of this matrix will be overwritten with the resulting adjusted matrix, it is recommended to first do a copy. This matrix must not be write protected.

dpq

Temporary matrix of type mf which is used to hold the gradient direction matrix. This matrix must exist and must not be write-protected. Its initial contents will be lost.

iter

Number of iterations stopping criteria used in assignment.

relgap

Relative gap stopping criteria used in assignment.

normgap

Normalized gap stopping criteria used in assignment.

gstep

Number of gradient steps to be performed (adjustment iterations).

cnt

This is an optional argument. If set to 1, the first "half step" (i.e. a regular auto assignment to compute volumes) is skipped, assuming that this assignment was already performed. Use this option only when continuing with more steps on the same adjustment (i.e. higher <gstep> value).

Besides the explicit parameters, the DEMADJ macro assumes some implicit requirements on the data base. The following link user data items and scalar matrices are used by the macro:

ul1

Observed volumes (0=no count available)

ul3

Reserved for temporary storage. Original contents will be lost.

ms90

This scalar contains the current adjustment step number. If it exists, it must be initialized to 0 before a new adjustment is started. This scalar will be incremented after each adjustment step. It is compared with the gstep stopping criterion at each iteration.

ms91-ms94

Scalars to hold the value of the objective function Z, the maximum gradient, the optimal step length and temporary data. These scalars are created if they do not exist. If they do exist, their original contents will be lost.

Even though only fixed demand assignments are carried out, it is also recommended that the DEMADJ macro is used with the variable demand version of the auto assignment (see also the section Bugs+Fixes in this issue). In addition to the above, the macro itself contains more detailed instructions in the initial comment section, which should be read and observed carefully.